Jason Kamin
Modern Astrophysics
Astro 335
Steve Schneider

Lunar Recession

Abstract

The radial velocity of the moon away from the Earth was mathematically determined to be 3.53 cm per year.  This expansion of the orbital semi-major axis is directly coupled with the slowing of the rotation of the Earth, mathematically determined to be -4.3×10^-22 s^-2.  These effects are due to mostly to tidal friction and the conservation of angular momentum of the Earth-moon system.  The system will asymptotically approach equilibrium with a limit of the semi-major axis of the moon at about 2.2 times its current distance in about 30 billion years.

Introduction

            Humans have always held a fascination with the moon.  It has been the focus of fables and legends for thousands of years.  From werewolves to astrology geology, people seem to have an innate interest in the moon.  Some are convinced we never landed on it, others believe that life may reside there.  So many biological life cycles depend on it’s passing through the sky, from sea turtles laying eggs to reproductive cycles of fish, we are forced to take more than a passing interest in this amazing satellite of Earth. 

            The moon is a unique satellite in the solar system.  First, we believe that it was probably formed by a massive body, probably about the size of Mars, colliding with the Earth early in the formation of the solar system.  This Mars size object ejected large amounts of the Earth’s mantle into orbit around the Earth.  This material eventually coalesced into the present day moon.  Another strange thing about the moon is its size relative to the Earth.  The mass of the moon is about 1.2% the mass of the Earth, and its diameter is about 25% that of the Earth, by far the largest percentages of any other planet-moon pair in the solar system.[1] 

Theory

The moon orbits the Earth once every 27.3 days.  As it spins around the Earth, the moon exerts a gravitational force on the planet.  The solid land of the Earth is not affected much by this force, however the ocean water is.  As the moon tugs on the water two bulges are created in the ocean, one facing the moon and the other directly opposite it.  These tides should follow the moon and be directly aligned with the moon as it orbits the Earth.  However, the situation is not quite this simple.

The Earth is also spinning on its own axis, once a day.  Therefore, the Earth’s angular velocity is much faster than the moon’s.  The ocean water is being dragged along with the Earth as it spins but the tidal bulges are always trying to stay directly underneath the moon.  As the moon tries to pull the water back underneath it, the water dragging back along the ocean floor creates a frictional force.  Therefore, the tidal bulges are constantly being tugged ahead of the moon by the Earth’s rotation. 

Figure 1

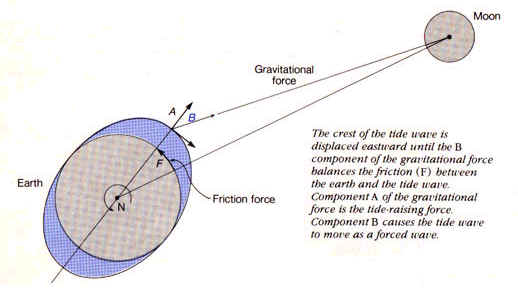
            Newton’s Second Law states that for every action there is an equal and opposite reaction.  Therefore, as the moon tugs back on the tidal bulges, the tidal bulges, in turn, pull on the moon with a little bit of a force parallel to the rotation of the system.  This tidal acceleration is actually trying to speed up the velocity of the moon.  This puts the moon in a position where its orbit is spiraling outward away from the Earth.  At the same time, the tidal bulges are constantly being slowed in their rotation with the Earth.  Therefore, the Earth is, in effect, plowing through the water.  The frictional forces of the ocean water are slightly slowing the Earth’s rotation. 

            The moon’s angular frequency is dependant only on its orbital semi-major axis.  As the moon gets farther away, it orbits more slowly.  While the Earth’s angular frequency is getting slower also, its acceleration is more negative than the moon’s is.  As a result, the Earth’s angular frequency should asymptotically approach the moons over time.  Eventually, the system should be close enough to this limit to be considered stabilized.  At this point in time, the Earth and the moon will be completely tidally locked.  This means that the same side of the Earth will always face the moon. 

            The total energy of the Earth-moon system is not constant.  It is losing energy due to the tidal friction.  The angular momentum of the Earth is decreasing, since the Earth’s rotation is slowing.  The angular momentum of the moon is increasing since its orbital semi-major axis is increasing.  The one thing that is constant, however, is the total angular momentum of the entire Earth-moon system.  The Earth’s spin angular momentum is being transferred to the moon’s rotational angular momentum.  This is the key that let’s us try to extrapolate forward and backward through time.

Procedures

            There are 3 observed parameters that I started with other than fundamental and physical constants.  Everything else can be derived from the laws of physics.  The angle by which the tidal bulges leads the moon today (Eq. 3), the height of the tidal bulge (Eq. 4), and the tidal energy dissipation rate (Eq. 48) are all observed parameters.

            In order to determine the torque on the tidal bulges (Eq. 11) due to the tidal acceleration (Eq. 7), I needed the mass of the bulges.  I assumed the mass to be 70% water and 30% earth.  This is not necessarily a reasonable assumption; I used these percentages because they are the percentages of the surface of the Earth that is covered in each.  Dividing the torque by the rotational inertia of the Earth (Eq. 13), I was able to determine the angular acceleration of the Earth to be -4.301 radian×s^-2, which is equivalent to the day getting longer by  -0.0043 s/century (Eq. 14). 

In order to determine the radial velocity of the moon I set the derivative of the total angular momentum with respect to time equal to zero (Eq. 27a) (Conservation of Angular Momentum) and then solved for the radial velocity (Eq. 27b).  The current radial velocity of the moon is 3.53 cm/yr (Eq. 28).

In order to devise a way to extrapolate through time and see what happens to the system I relied heavily on the Conservation of Angular Momentum.  The current angular energy and the angular momentum of the system can be determined (Eq. 33, 34).  We know that the angular energy will change will change as a function of both the angular momentum of the moon and the angular momentum of the Earth (Eq. 37).  However, the angular momentum of the Earth can be written as a function of the angular momentum of the moon, which in turn can be written as a function of the semi-major axis of the moon’s orbit.  Therefore, the difference in energy from the current energy can be expressed as a function of the mean distance (Eq. 38).  This dependence is plotted in Figure 2.

When the angular energy stops changing, then we know that the system has stabilized.[2]  I visually determined this distance from the graph to be about 2.2 times the current distance (Eq. 39).  I then used a solve block to solve for the angular velocity of the Earth at 2.2×d_now (Eq. 41).  The length of a day on Earth when the system has stabilized is ~38 current days (Eq. 42) and the length of the semi-major axis of the moon’s orbit will be ~132 earth radii (Eq. 43).

The Roche Limit is the minimum distance that a natural satellite can orbit a body.  This value depends on the densities of both bodies.  I calculated this value for the moon and the Earth and found it to be ~5% of the current distance (Eq. 47). 

The third observed parameter that I exploited was the current rate of energy loss due to tidal dissipation (Eq. 48).  This value is 4 billion W.  Since I have no way of determining this rate as a function of distance, I created a function that equaled 4 billion W at the current distance using only variables that I had already been dealing with (Eq. 50).  Using this function (Eq. 51), Figure 3 shows the rate of energy loss due to tidal dissipation as a function of distance. 

            Finally, in order to get the time that it would take for the moon to move between two distances I created another function (Eq. 52) that gives the time as a function of two distances.  This is plotted in Figure 4.

Data Analysis

            There are many places that error crept into my method.  The first glaring error is in the function that I created for the rate of energy loss due to tidal dissipation.  This is a completely made up function that seems to work well for large distances but horribly for any distance under about 0.8×d_now.  This is because the rate of energy loss function blows up much faster at small distances than the energy difference function does.  It seems somewhat reasonable at first glance since it seems to be the right shape, but unfortunately it doesn’t work.  Without knowing how the tidal dissipation actually works this problem is really difficult. 

            More error may have leaked in from the assumption that tidal frictional forces are the only ones at work.  This is a complex system involving a lot more variables than I pretend in this analysis.  Once again, this is probably too complicated to have a simple model be accurate. 

            Nevertheless, most of the numbers that I calculated are actually fairly accurate.  I found the length of a day to be increasing by -0.0043 s/century. The actual observed value of this is (-0.0020 ± 0.0002) s/century.  This is a reasonable amount of error considering the size of the numbers that we are dealing with.  I found the radial velocity of the moon to be 3.53 cm/yr.  The observed value is

(4.4 ± 0.6) cm/yr.  Again, this is fairly accurate.[3] 

            I calculated the system to be nearly in equilibrium at a distance of about 2.2 current lunar distances in about 30 billion years.  This seems to be consistent with more technical articles.[4] 

            Unfortunately, because of my incorrect rate function I was not able extrapolate backwards through time.  Figure 4 shows that at distances of less than about 0.8×d_now the results become nonsensical. 

Conclusion

The estimate for the length of time that it will take for the system to be nearly stabilized is far longer than the Main-Sequence lifetime of the sun (~5 billion years).  Therefore, this is not a problem that we have to worry about.  The moon will never be tidally locked with the Earth. 

            Since the mean distance between the Earth and moon is getting greater with time, it is reasonable to assume that the moon was much closer in the past.  In fact, it is perfectly logical to assume this when considering the system we have been dealing with.  This is very interesting.  The height of the tides varies inversely with the cube of the distance to the moon.  Therefore, if the moon were 5 times closer (~0.2×d_now) then the tides would be 125 times higher.  So, when the moon was much closer, the oceanic tides were also much bigger and they moved around the planet much faster also. 

            Tides of this size speeding around the world would have scraped and pounded against the primeval earth, mixing up all of the ingredients of the planet into an oceanic carbon-based soup.  It is possible to imagine this kind of chaos early in the Earth’s formation potentially being the catalyst for life developing.  If this were the case, then life in the galaxy might be more rare than we now believe it to be.  Maybe having a moon of our relative size being very close early in the formation of the planet and then becoming much less chaotic as it moves farther out makes us somewhat unique.  This could have implications that could philosophically change how we look at ourselves, a small blue-green oasis of life in a vast, empty cosmos. 

EQUATIONS AND ADDITIONAL FIGURES