Jason Kamin
Advanced Physics Lab
Physics 350
Prof. Decowski

Half-life of ²¹²Po

Abstract

We measured the average time it took for an alpha decay to occur changing ²¹²Po into ²⁰⁸Pb as part of the ²³²Th decay chain.  We took measurements for 3 days and were able to determine the half-life of ²¹²Po to be 313 ± 4 ns.

Introduction

            The goal of this experiment is to measure the half-life of polonium-212.  The expected half-life for ²¹²Po is very short (about 300 ns) so in principle it would be very difficult to measure this lifetime.  However, it is not so hard if we have a source that is constantly producing ²¹²Po.  It especially becomes a manageable task if the decay series is one that doesn’t contain other decays that are on a comparable time scale.  Fortunately, thorium-232 possesses just such a decay chain (Diagram 7).  The next-shortest half-life in the chain is about 0.16 s (²¹⁶Po), more than 10⁵ times longer than the decay that we are interested in.  This gives us an excellent opportunity to study the ²¹²Po alpha decay half-life.

Theory

            A suitable ²³²Th source is not easy to find.  However, an older type of gas lantern mantle, which can be found in a Mexican marketplace, contains a significant amount of this element and is an excellent source.  Thorium decays predictably through five a and three b decays into ²¹²Bi.  ²¹²Bi, however, is not a stable isotope and 1/3 of the time it decays into ²⁰⁸Tl and then ²⁰⁸Pb, the stable end to the decay chain.  The other 2/3 of the time ²¹²Bi decays to ²¹²Po, the isotope that we are interested in, which in turn releases one last a particle and then also decays into ²⁰⁸Pb.

            In order to examine these ²¹²Po decays we use scintillation detectors.  A scintillation detector consists of a scintillating crystal and a photomultiplier.  When a nuclear particle or radiation enters the scintillating crystal it excites atoms in the crystal.  As the atoms drop back down to their ground state they emit photons.  These photons enter the photomultiplier and are converted into a weak current of photoelectrons.  An applied voltage inside the photomultiplier creates a potential, which accelerates the photoelectrons and slams them into an anode producing many additional electrons.  This process is repeated many times in the photomultiplier creating a cascade-like effect of electrons.  When they reach the end of the photomultiplier there are enough electrons to produce a measurable pulse of current. 

Procedures

The scintillating crystal is placed in front of the photomultiplier.  To ensure a proper propagation of the photons from the scintillating crystal to the photomultiplier, we applied a thin layer of silicon gel to serve as an interface between the crystal and the photomultiplier lens.  We wrapped the gas lantern mantle around the scintillating crystal.  The end of the photomultiplier that housed the crystal and the mantle was wrapped in aluminum foil to hold the mantle in place over the crystal and the entire apparatus was placed in a wooden box that was painted black.  The box was also wrapped in aluminum foil.  This was done to help prevent interference from external light and electromagnetic waves. 

We attached two cables to the photomultiplier.  One of them supplied the voltage to the photomultiplier and the other carried the output signal to the Constant Fraction Discriminator (CFD) through a Timing Filter Amplifier (TFA).  The TFA served two purposes; it amplified the signal and shaped the pulse.  The CFD uses the threshold method to measure the pulses.  Whenever the input signal is above a certain magnitude, the CFD will recognize it.  This creates a problem.  If two pulses of different magnitudes come at the same time, then the CFD will measure the larger one as arriving first.  Therefore, we need to take 80% of the fall time of the pulse and delay the pulse by that amount.  By adding the attenuated original pulse and the delayed, inverted pulse we get a zero crossing point whose time does not depend on the pulse amplitude.  The unit produces a standard negative pulse at the zero crossing point time. 

            The two short pulses from the CFD outputs are fed into the Octal Gate Generator (OGG).  We calibrated the OGG to delay the start pulse more than the stop pulse.  That makes the stop pulse register about 100 ns before the start pulse.  Therefore, when the pulse from a ²¹²Bi decaying to a ²¹²Po hits the TAC, a stop registers (which does nothing since the timer has not been started yet) and then, afterwards, the start registers (which starts the timer).  When the pulse from the decay hits the TAC a stop registers, which stops the timer.  The following start pulse does nothing because the TAC is still processing the measurement.  The TAC only registers a measurement when the two pulses are within ~10 ms.  The TAC then takes the time duration and converts it to a pulse with an amplitude that directly corresponds to the lifetime of a ²¹²Po atom. 

            The delay supplied by the OGG does not matter.  The average lifetime (t) of a ²¹²Po is described by an exponential function.  Therefore the offset is filtered out as a constant (See Diagram 6). 

            The output from the TAC is fed into and recorded by the Multichannel Analyzer (MCA).  The TAC output, however, is a positive signal and the MCA registers negative pulses.  Therefore, as a final step, we must invert the output signal from the TAC before we feed it into the MCA.  Also, the MCA needs a signal to tell it to measure the signal so we have two outputs coming from the TAC through the inverter feeding into the MCA.  One acts as a gate, telling the MCA when to measure.  The other is the actual signal to be measured. 

            There was enough ²³²Th in our lantern mantle that we only needed to let this experiment collect data for about three days. 

Data Analysis

            In order to calibrate the MCA we measured specific time intervals and recorded what channels they corresponded to.  Plotting these, we were able to find a calibration function to convert a channel to the corresponding time, (Diagram 1).  Using this calibration function we first convert all the channels over to these corresponding times. 

            We looked at the first and last 200 channels to see where our reliable measurements start and stop.  We determined that between channels 45 and 1985 was where our good data resided.  We also wanted to get rid of all of the blank channels because blank channels will spoil our function-fitting algorithm.  So we need to compress the 1940 channels to 194 channels.  We will just add up all of the counts within a 10-channel span and count that as one compressed channel.  This effectively gets rid of any blank channels.  This increases our error in our time estimation but not enough to be concerned about. 

            We ran Mathcad’s algorithm for determining the parameters for an exponential function of the form 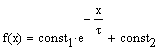, where const₁, const₂, and t are constants.  The fit, however, was not very good.  Suspecting that we might be measuring two different decays, we tried to fit the data to a combination of two exponential functions .  t₁ is the average time that it takes ²¹²Po to decay, (Diagram 2), and t₂ is the average lifetime of the unknown decay.  This function fit our data very well.  In order to extract the half-life (t_½) from t, we need to multiply t by ln(2), (Diagram 6). 

            To account for the statistical error in this analysis, we wrote a function that would weight the points according to their respective error; points that had a smaller associated error would be weighted more heavily.  Since we didn’t know how much overall weight to use, we ran the entire program using several different errors weights.  Plotting these errors, it became apparent that the resultant ²¹²Po half-life stabilized with an overall weight of about 3 x 10⁵, (Diagram 3).  Therefore, we used this overall weight to analyze the data. 

In order to determine the error of our t, we took these final numbers to Sigma Plot and ran the Sigma Plot function fitting process, (Diagram 8).  The advantage to Sigma Plot is that it gives an associated error for each parameter that it determines.  The parameters that Sigma Plot yielded were identical to Mathcad’s.  We found t to be 451 ± 5 ns, thereby making t_½ = 313 ± 4 ns, (Diagram 4).

Conclusion

            We analyzed the data for this experiment with three different programs: Professor Decowski’s Linux algorithm (Diagram 9), Mathcad, and SigmaPlot.  The three analyses all agree.  We found the half-life of ²¹²Po to be 313 ± 4 ns.  This is in perfect agreement with the accepted value of 310 ns[1]. 

            These measurements for the ²¹²Po decay are excellent, but we cannot ignore the additional unknown decay that we are detecting.  A t value of 2.1 leads to a half-life of about 1.46 ± .02 ms.  We scanned half-life tables to find all of the known decays with half-lives between 1 and 2 ms.  We were able to eliminate most of the potential candidates because they occurred in a decay chain that was not naturally occurring.  The few promising candidates that we could identify were all related to the thorium fission decay chain.  Hoping that this would resolve our mystery, we estimated how many of these thorium fissions we could expect to find coming from our thorium sample if cosmic rays were inducing this fission process.  Unfortunately, we found that we were detecting ~10⁵ times more decays than we could expect from this process.  Therefore, this remains an unsolved mystery that begs further analysis in the future.   

Click here for Diagrams